Lecture 5 - Algebraic reconstruction methods

So far, we have seen 2 image reconstruction methods:

• Fourier reconstruction
• Filtered back projection

These may not perform optimally when the sinogram is undersampled or noisy. We therefore consider an alternative, which attempts to solve the system of equations explicitly.

Overview

• Richardson iteration
• Row-action methods
• Assignments

Richardson iteration

We can attempt to solve a linear system of equations

$$Ku = f,$$

using the Richardon iteration

$$u^{(k+1)} = u^{(k)} - \alpha K^T(Ku^{(k)} - f).$$

When $u^{(0)} = 0$ and $0 < \alpha < 2/\|K\|^2$ it converges to the minimum-norm solution of the normal equations

$$K^T\!Ku = K^Tf.$$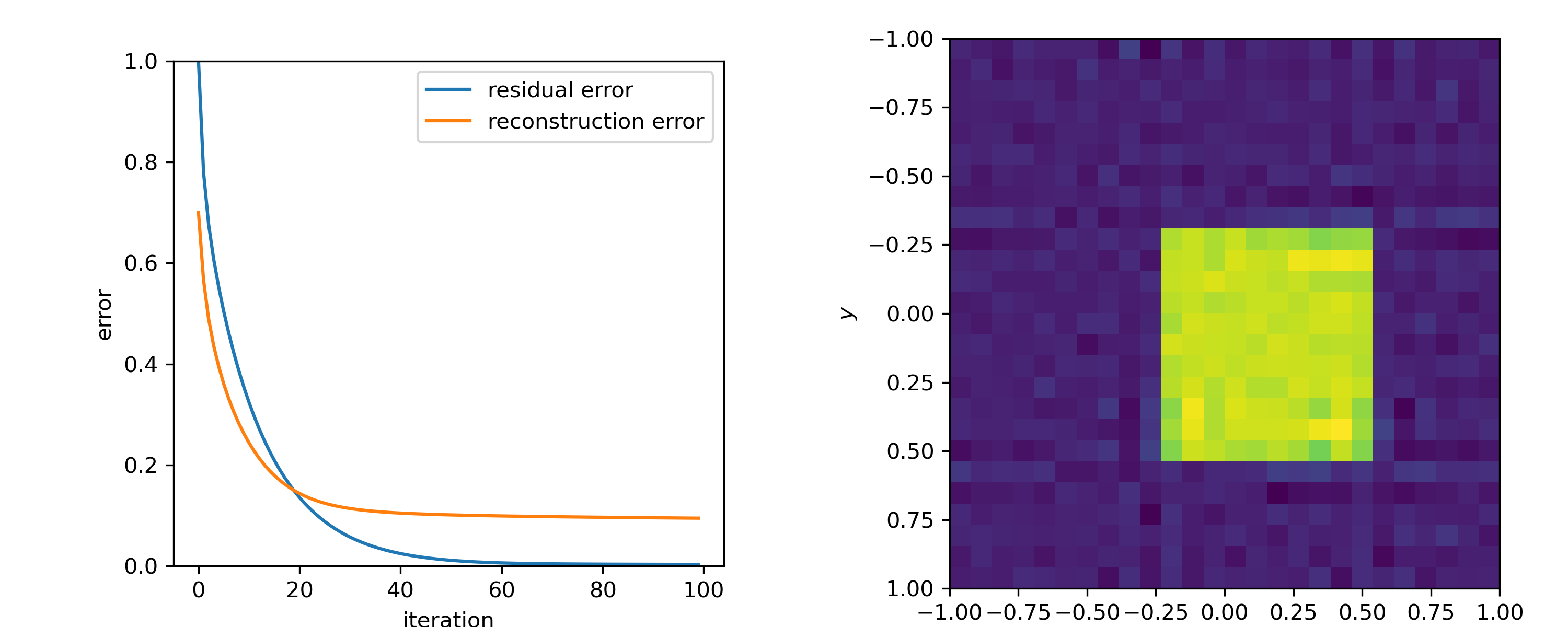

Convergence

Convergence to a solution of the normal equations:

$$e^{(k+1)} = \left(I - \alpha K^T\!K \right)e^{(k)},$$

so error components corresponding to eigenvalues $\approx \alpha^{-1}$ decay fastest.

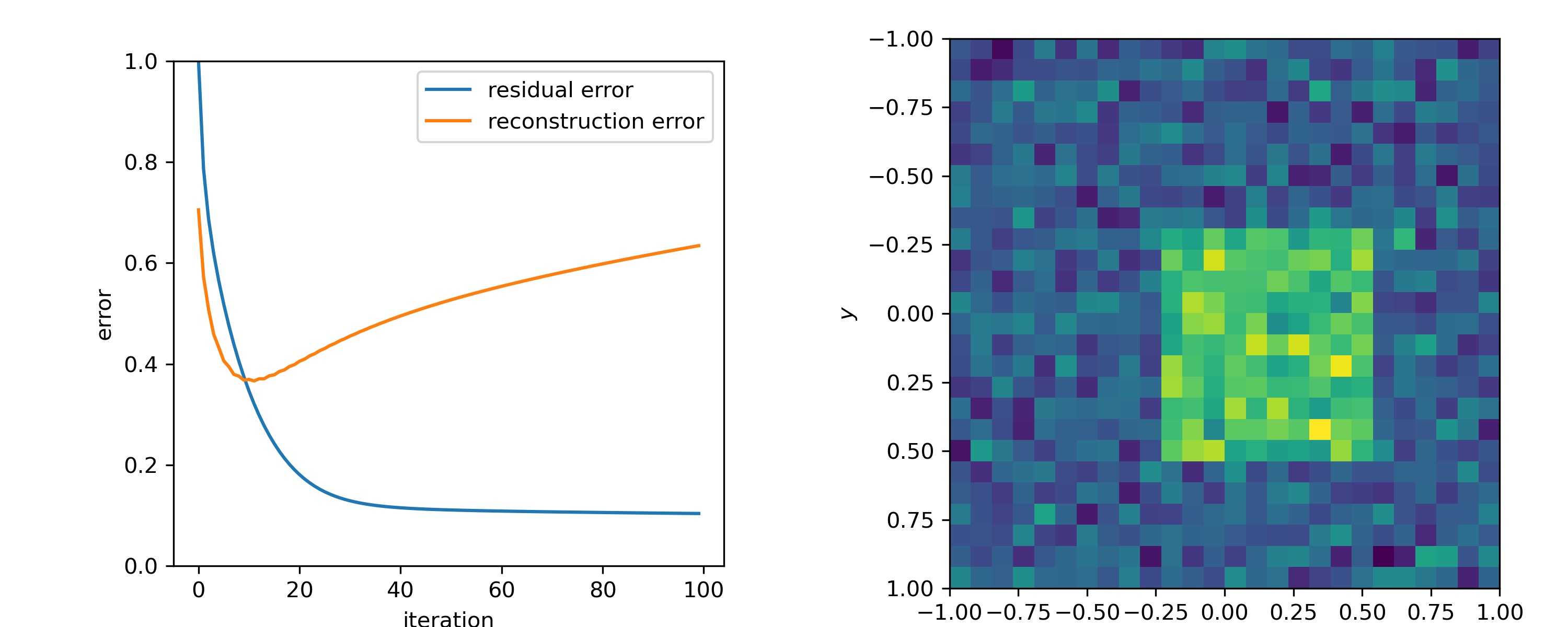
Convergence to the true solution:

$$e^{(k+1)} = \left(I - \alpha K^T\!K \right)e^{(k)} - \alpha K^T\epsilon.$$

Computing the steplength

• Determine $\alpha$ such that the eigenvalues of $\left(I - \alpha K^T\!K \right)$ are $\in (-1,1)$
• let $\alpha \in (0, 2/\lambda_\max (K^T\!K) )$
• use that $(K^T\!K)^k v$ tends to largest eigenvector of $K^T\!K$ as $k\rightarrow \infty$
• use $\|K\|_2^2 \leq \|K\|_1 \|K\|_\infty$.

Row-action methods

The computational cost of Richardson's method is dominated by the cost of the foward and adjoint Radon transform. Can we work with a single ray at a time?

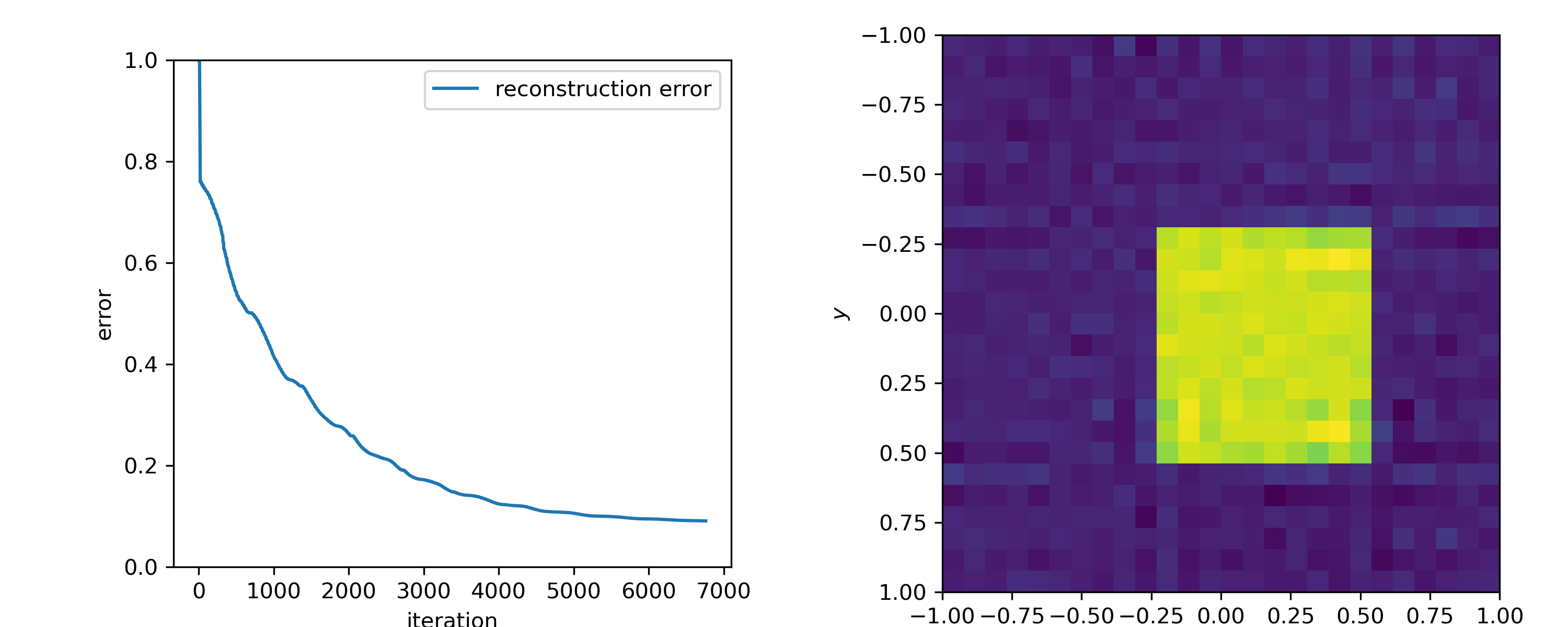
The Kaczmarz method proceeds as follows:

$$u^{(k+1)} = u^{(k)} - \frac{f_i - k_i^Tu^{(k)}}{\|k_i\|_2^2} k_i^T,$$

with $k_i$ the $i^{\text{th}}$ row of $K$.

Convergence

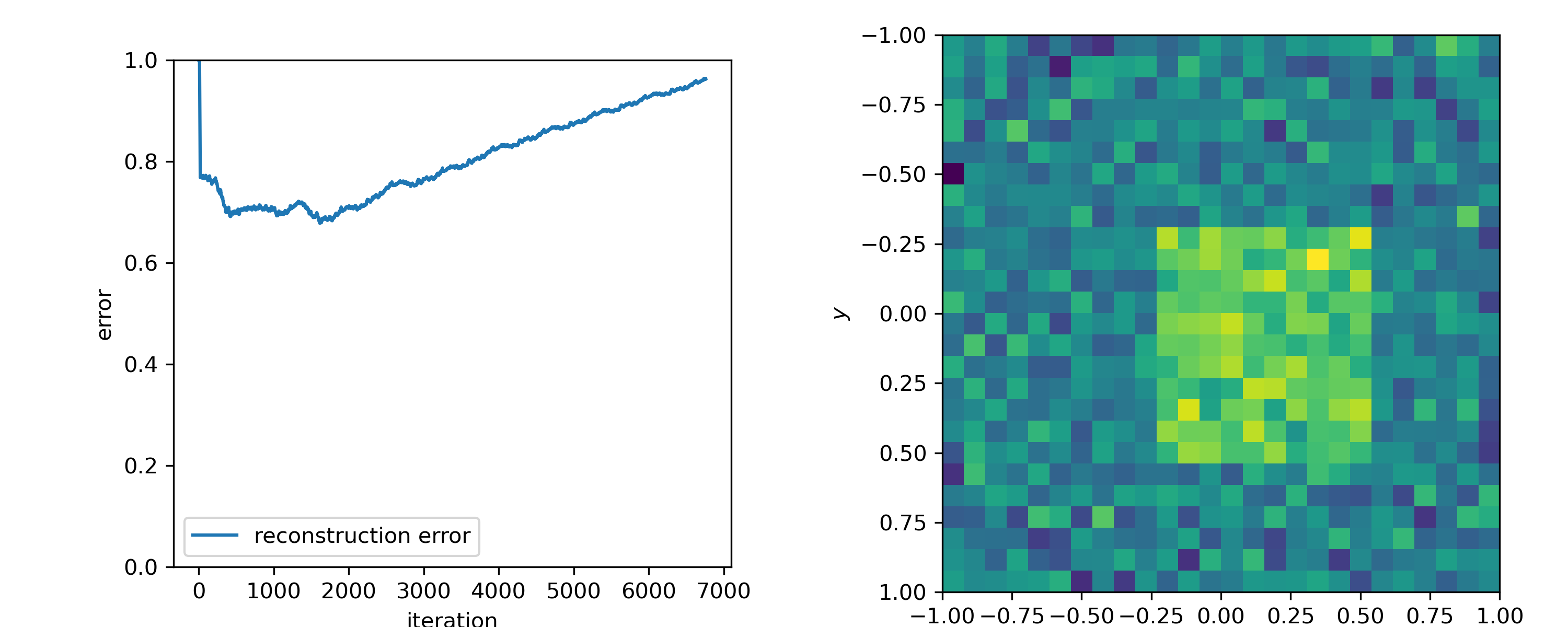
• Many results when system is consistent
• May not converge when system is inconsistent
• Relaxed version converges to solution to weighted least-squares problem

Assignments

Assignment 1

Compare the iterative methods introduced in this lecture with the previously defined reconstruction methods in terms if computational efficiency and reconstruction quality.